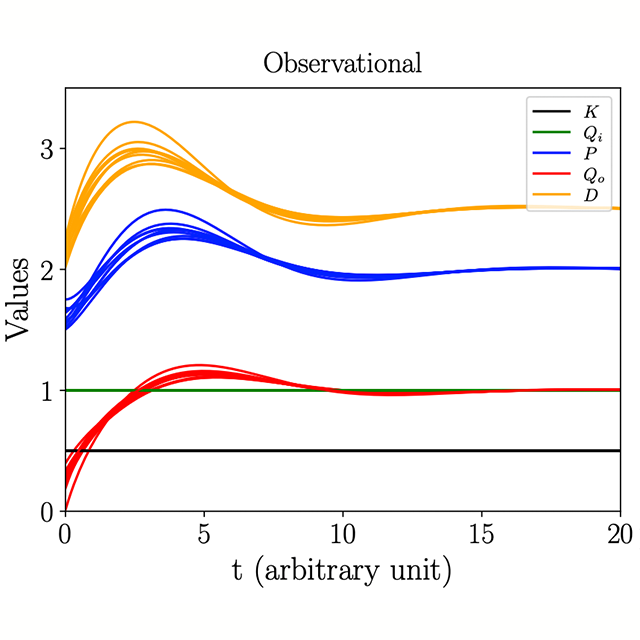
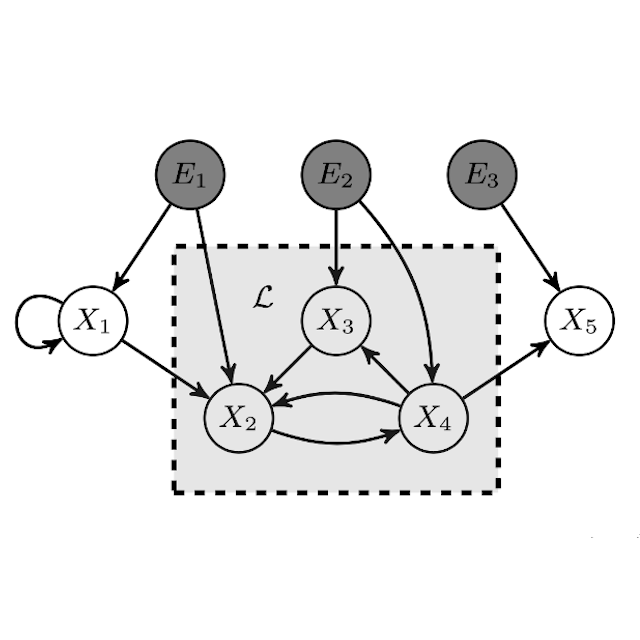
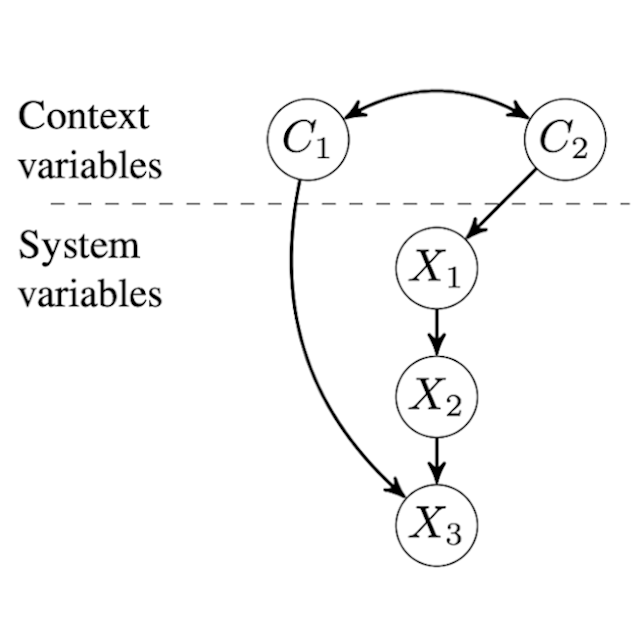
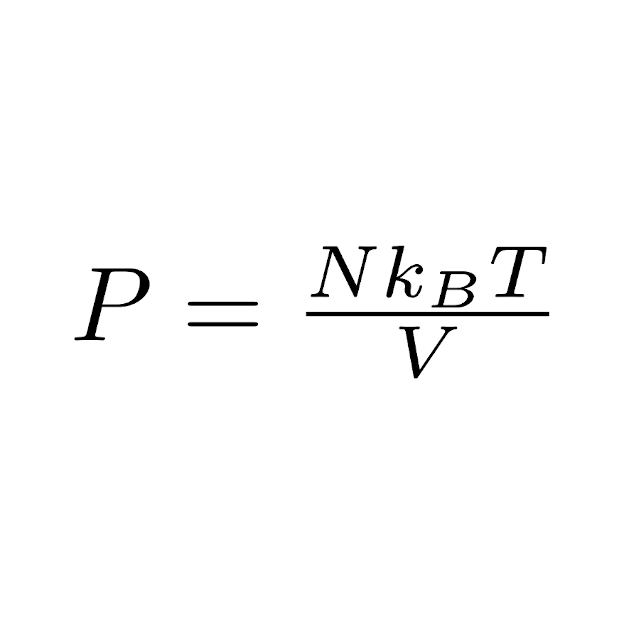I am a postdoctoral researcher at the Sequential Decision Making group at the Delft Univeristy of Technology in the Netherlands.
I am broadly interested in statistics, machine and reinforcement learning, with an eye towards causal, sequential and anytime-valid inference.
I have obtained my PhD in causal modeling at the University of Amsterdam, advised by Prof. Joris M. Mooij. Prior to that I studied Mathematics and Physics at the Utrecht University, where Dr. Urs Schreiber was my thesis advisor. During my studies I had a short interlude in particle physics research at CERN.
For the most up-to-date publication list, see my Google Scholar page.